5 من “انواع شبه المنحرف” وقوانين مساحة شبه المنحرف

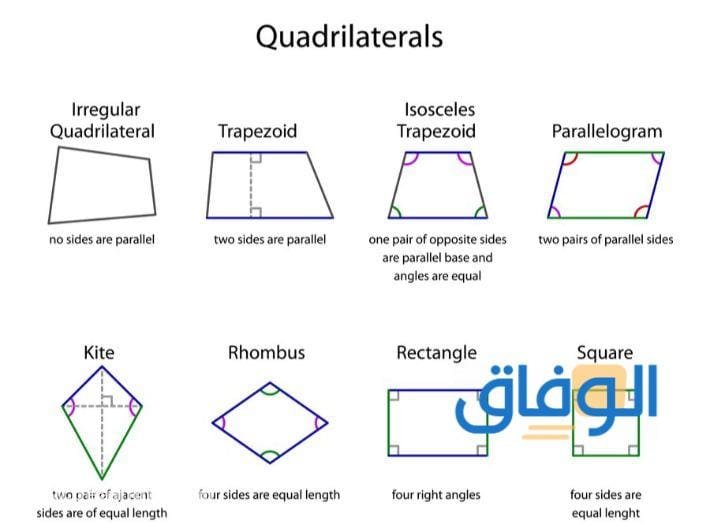
انواع شبه المنحرف الذي يعتبر واحد من من الأشكال الهندسية المتعارف على أنها تتكون من أربعة أضلاع، ويحظى بالعديد من الخصائص والصفات المميزة له عن باقي الأشكال، وهذا ما سوف يدور حوله هذا المقال الذي يفيد في تحديد أهم هذه الأنواع وما هي القوانين الخاصة التي يمكن من خلالها حساب كل من قيمة المساحة المحددة له وقيمة المحيط الإجمالي له.

انواع شبه المنحرف

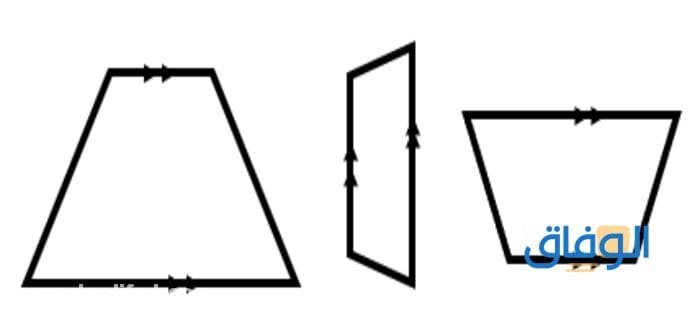
الإجابة على تساؤل ما هي انواع شبه المنحرف المنتظم رباعي الأضلاع، نوفرها بالتفصيل خلال ما سوف نقوم بعرضه من شرح عبر الجدول التالي:

نوع شبه المنحرف
التفصيل

قائم الزاوية
يحتوي زاوية قائمة تساوي 90° تنتج من تقاطع قاعدته مع الارتفاع.

حاد الزاوية
يحتوي زاويتين حادتين نتيجة تقاطع أطراف القاعدة مع ارتفاعاته، وقياسهما أقل من 90°.

منفرج الزاوية
يضم على زاوية واحدة منفرجة تنتج من تقاطع قاعدته مع أحد الارتفاعات، وقياسهما أكبر من 90°.

متساوي الساقين
يحتوي على ساقين متساويين في الطول، بالإضافة إلى قاعدتين متوازيتين وغير متساويتين في الطول.

مختلف الأضلاع
يحتوي على أربعة أضلاع غير متساوية في الطول، اثنين منهما هما القاعدتين المتوازيتين.

أهم خصائص شبه المنحرف

يعد التعرف على جميع انواع شبه المنحرف، يأتي الدور الآن على الإحاطة بأهم الخصائص الرياضية المميزة له والتي تعد سمة مشتركة ما بين جميع أنواعه ما عدا النوع المتساوي الساقين، وهذه الخصائص هي التالي:

• كلا القاعدتين في شبه المنحرف متوازيتان.
• إجمالي قياسات زوايا شبه المنحرف الداخلة هي 360 درجة.
• مجموع كل زاويتين متجاورتين في شبه المنحرف هي 180 درجة.

اقرأ أيضاً: الفرق بين مربعين

قوانين حساب مساحة شبه المنحرف

لابد من التعرف على بعض القوانين الخاصة بمساحة الشكل الهندسي شبه المنحرف التي يمكن من خلالها إيجاد حل لجميع المسائل الحسابية والرياضية التي تضمن هذا الشكل، ويوجد عدد اثنين من القوانين الخاصة بذلك سوف نقوم بتوضيحها من خلال التالي

القانون الأول

• يتم الاعتماد فى هذا القانون على كل من طول القاعدتين والارتفاع.
• ينص القانون على أن مساحة شبه المنحرف = ½ × مجموع طول القاعدتين × الارتفاع.
• أي مساحة شبه المنحرف = ½ × ( أ+ب) × ع.

القانون الثاني

• يعتمد في هذا القانون الذي يطلق عليه كذلك اسم قانون هيرون على أطوال أضلاع شبه المنحرف ونصف قيمة محيط شبه المنحرف.
• حيث يتم التعبير عن مساحة شبه المنحرف بالمعادلة التالية، مساحة شبه المنحرف= (ب+أ)/(|ب – أ|)×الجذر التربيعي للقيمة ((س – ب) × (س – أ) × (س – ب – جـ) × (س – ب – د))، حيث إن ب هو رمز طول القاعدة السفلية، أ هو رمز طول القاعدة العلوية، س هي نصف قيمة المحيط، ج هي طول الساق الأولى، د هي طول الساق الثانية.

اقرأ أيضاً: مساحة شبه منحرف غير منتظم

قوانين حساب محيط شبه المنحرف

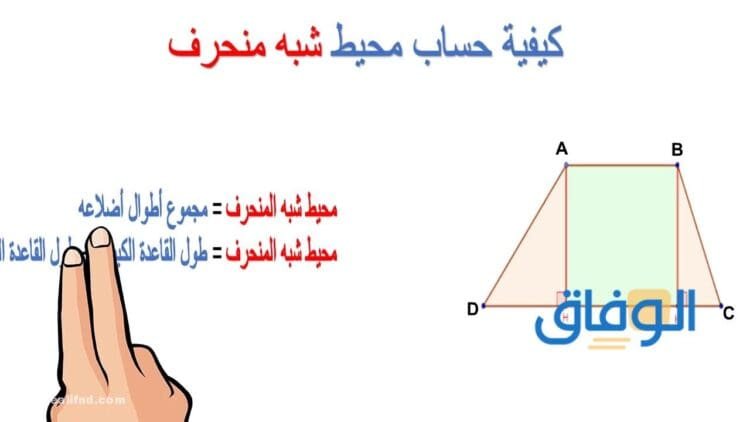
بعد العلم بالقوانين الخاصة بمساحة شبه المنحرف سوف نستكمل الآن باقي القوانين الخاصة به والتي من أهمها القوانين المحددة لقيمة محيط شبه المنحرف، والتي يوجد منها عدد اثنين من القوانين هي التالي:

القانون الأول

• يلجأ هذا القانون إلى الاعتماد على كل من أطوال أضلاع شبه المنحرف.
• يأتي نص هذا القانون في الصورة التالية: محيط شبه المنحرف= طول القاعدة العلوية والسفلية + طول الضلعان غير المتوازيين.
• أي أن محيط شبه المنحرف= أ + ب + جـ + د.

القانون الثاني

• يتم استخدام كل من طول القاعدتين السفلية والعلوية، والارتفاع، والزوايا المحصورة بين القاعدة السفلية والساقين، في هذا القانون.
• يكون النص الكامل لهذا القانون هو التالي: محيط شبه المنحرف= أ+ب+ع×((1/جاس) + (1/جاص))، حيث إن أ هو رمز طول القاعدة العلوية، ب هو رمز طول القاعدة السفلية، ع هو رمز الارتفاع، س هي الزاوية المحصورة بين القاعدة السفلية والساق الأولى، ص هي الزاوية المحصورة بين القاعدة السفلية والساق الثانية.

اقرأ أيضاً: معلومات عن الرياضيات

قدمنا شرح مفصل عن جميع انواع شبه المنحرف بالإضافة إلى التعرف على جميع الخصائص الرياضية الخاصة به، بجانب تحديد أهم القوانين الهامة والبسيطة لحساب كل من مساحته ومحيطه بشكل دقيق.